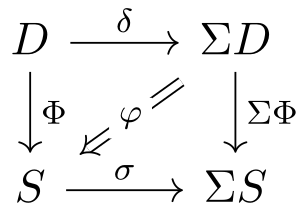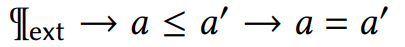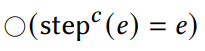publications
2026
- đź“„ POPL
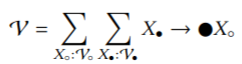Abstraction Functions as TypesHarrison Grodin, Runming Li, and Robert HarperJan 2026Software development depends on the use of libraries whose public specifications inform client code and impose obligations on private implementations; it follows that verification at scale must also be modular, preserving such abstraction. Hoare’s influential methodology uses abstraction functions to demonstrate the coherence between such concrete implementations and their abstract specifications. However, the Hoare methodology relies on a conventional separation between implementation and specification, providing no linguistic support for ensuring that this convention is obeyed. This paper proposes a synthetic account of Hoare’s methodology within univalent dependent type theory by encoding the data of abstraction functions within types themselves. This is achieved via a phase distinction, which gives rise to a gluing construction that renders an abstraction function as a type and a pair of modalities that fracture a type into its concrete and abstract parts. A noninterference theorem governing the phase distinction characterizes the modularity guarantees provided by the theory. This approach scales to verification of cost, allowing the analysis of client cost relative to a cost-aware specification. A monadic sealing effect facilitates modularity of cost, permitting an implementation to be upper-bounded by its specification in cases where private details influence observable cost. The resulting theory supports modular development of programs and proofs in a manner that hides private details of no concern to clients while permitting precise specifications of both the cost and behavior of programs.
2024
- đź“„ MFPS
Amortized Analysis via CoalgebraHarrison Grodin, and Robert HarperDec 2024Amortized analysis is a cost analysis technique for data structures in which cost is studied in aggregate: rather than considering the maximum cost of a single operation, one bounds the total cost encountered throughout a session. Traditionally, amortized analysis has been phrased inductively, quantifying over finite sequences of operations. Connecting to prior work on coalgebraic semantics for data structures, we develop the alternative perspective that amortized analysis is naturally viewed coalgebraically in a category of cost algebras, where a morphism of coalgebras serves as a first-class generalization of potential function suitable for integrating cost and behavior. Using this simple definition, we consider amortization of other sample effects, non-commutative printing and randomization. To support imprecise amortized upper bounds, we adapt our discussion to the bicategorical setting, where a potential function is a colax morphism of coalgebras. We support algebraic and coalgebraic operations simultaneously by using coalgebras for an endoprofunctor instead of an endofunctor, combining potential using a monoidal structure on the underlying category. Finally, we compose amortization arguments in the indexed category of coalgebras to implement one amortized data structure in terms of others.
- đź“– Notes
- đź“„ POPL
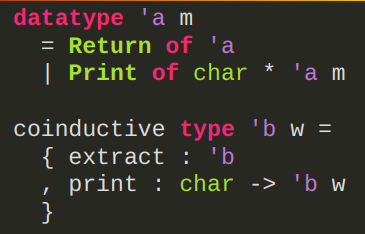
Decalf: A Directed, Effectful Cost-Aware Logical FrameworkJan 2024We present decalf, a directed, effectful cost-aware logical framework for studying quantitative aspects of functional programs with effects. Like calf, the language is based on a formal phase distinction between the extension and the intension of a program, its pure behavior as distinct from its cost measured by an effectful step-counting primitive. The type theory ensures that the behavior is unaffected by the cost accounting. Unlike calf, the present language takes account of effects, such as probabilistic choice and mutable state; this extension requires a reformulation of calf’s approach to cost accounting: rather than rely on a "separable" notion of cost, here a cost bound is simply another program. To make this formal, we equip every type with an intrinsic preorder, relaxing the precise cost accounting intrinsic to a program to a looser but nevertheless informative estimate. For example, the cost bound of a probabilistic program is itself a probabilistic program that specifies the distribution of costs. This approach serves as a streamlined alternative to the standard method of isolating a recurrence that bounds the cost in a manner that readily extends to higher-order, effectful programs.
The development proceeds by first introducing the decalf type system, which is based on an intrinsic ordering among terms that restricts in the extensional phase to extensional equality, but in the intensional phase reflects an approximation of the cost of a program of interest. This formulation is then applied to a number of illustrative examples, including pure and effectful sorting algorithms, simple probabilistic programs, and higher-order functions. Finally, we justify decalf via a model in the topos of augmented simplicial sets.
2023
- đź“ť Preprint
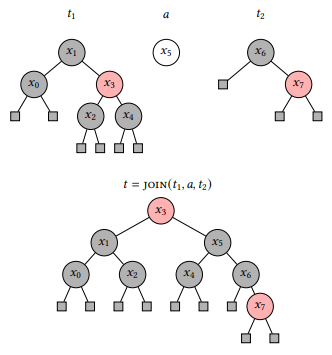A Verified Cost Analysis of Joinable Red-Black TreesRunming Li, Harrison Grodin, and Robert HarperSep 2023Ordered sequences of data, specified with a join operation to combine sequences, serve as a foundation for the implementation of parallel functional algorithms. This abstract data type can be elegantly and efficiently implemented using balanced binary trees, where a join operation is provided to combine two trees and rebalance as necessary. In this work, we present a verified implementation and cost analysis of joinable red-black trees in calf, a dependent type theory for cost analysis. We implement red-black trees and auxiliary intermediate data structures in such a way that all correctness invariants are intrinsically maintained. Then, we describe and verify precise cost bounds on the operations, making use of the red-black tree invariants. Finally, we implement standard algorithms on sequences using the simple join-based signature and bound their cost in the case that red-black trees are used as the underlying implementation. All proofs are formally mechanized using the embedding of calf in the Agda theorem prover.
- đź“„ CALCO
Amortized Analysis via Coinduction (Early Ideas)Harrison Grodin, and Robert HarperSep 2023Amortized analysis is a program cost analysis technique for data structures in which the cost of operations is specified in aggregate, under the assumption of continued sequential use. Typically, amortized analyses are presented inductively, in terms of finite sequences of operations. We give an alternative coinductive formulation and prove that it is equivalent to the standard inductive definition. We describe a classic amortized data structure, the batched queue, and outline a coinductive proof of its amortized efficiency in calf, a dependent type theory for cost analysis.
- 🗣️ PLunch
2022
- đź“„ POPL
A Cost-Aware Logical FrameworkJan 2022We present calf, a cost-aware logical framework for studying quantitative aspects of functional programs. Taking inspiration from recent work that reconstructs traditional aspects of programming languages in terms of a modal account of phase distinctions, we argue that the cost structure of programs motivates a phase distinction between intension and extension. Armed with this technology, we contribute a synthetic account of cost structure as a computational effect in which cost-aware programs enjoy an internal noninterference property: input/output behavior cannot depend on cost. As a full-spectrum dependent type theory, calf presents a unified language for programming and specification of both cost and behavior that can be integrated smoothly with existing mathematical libraries available in type theoretic proof assistants. We evaluate calf as a general framework for cost analysis by implementing two fundamental techniques for algorithm analysis: the method of recurrence relations and physicist’s method for amortized analysis. We deploy these techniques on a variety of case studies: we prove a tight, closed bound for Euclid’s algorithm, verify the amortized complexity of batched queues, and derive tight, closed bounds for the sequential and parallel complexity of merge sort, all fully mechanized in the Agda proof assistant. Lastly we substantiate the soundness of quantitative reasoning in calf by means of a model construction.
