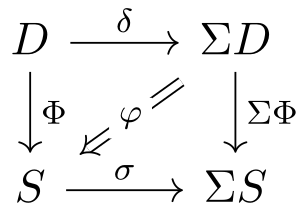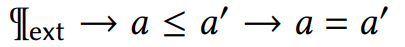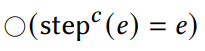Harrison Grodin

I’m a third-year Ph.D. student in the Principles of Programming group in the Computer Science Department at Carnegie Mellon University, advised by Robert Harper. My research is focused on programming language semantics, drawing inspiration from ideas in type theory and category theory.
Currently, I am developing Calf, a dependent type theory for verifying the cost and behavior of algorithms and data structures. Central themes in this project are effects, phase distinctions, exact and inexact bounds, and parallelism.
news
| Jul 2025 | 📝 publish a preprint about modular verification of algorithms and data structures |
|---|---|
| May 2025 | 📃 publish a post about amortized analysis and abstraction functions on the CMU CSD PhD blog |
| Apr 2025 | 🏆 receive the Alan J. Perlis Graduate Student Teaching Award |
| Dec 2024 | 📘 publish Amortized Analysis via Coalgebra in the Proceedings of MFPS XL |
| Dec 2024 | 🗣️ present at the Topos Institute Berkeley Seminar in Berkeley, CA |